BY ARTEM RASKIN
Disclaimer: All opinion articles posted on this website are solely the opinions of their author, and do not represent the opinions of the National Parliamentary Debate League or its Board of Directors.
You can use this forum thread to discuss the op-ed.
The formulas for calculating NPDL rankings, as described in Article XXI, can seem arbitrary at first glance. NPDL has a points calculator which walks students through how to calculate their own points - but not why points are calculated in this way. The goal of this article is to show that the formulas are not arbitrary at all, but are in fact derived from a few basic principles. The ranking system takes in tournaments of all shapes and sizes and brings them all to a common denominator.
Principle #1 - No debater should fall in the rankings because they attended a tournament.
Attending debate tournaments is good, even if you don’t win. So we don’t want our ranking system to ever discourage someone from attending a tournament. Debaters should gain points from tournament successes. Debaters should never lose points because they had an off tournament.
This rules out systems like ELO ratings, which punish debaters for losing rounds. ELO would incentivize debaters who qualify to TOC after the first few tournaments of the season to sit out the rest of the season and not push their luck.
Principle #2 - A qualification system should not discard useful information about tournament performance.
This rules out bid systems like the one used by Kentucky TOC. Say two bids are needed to qualify to the TOC. Say Alice attended 5 octas bid tournaments - she won the first one and lost in doubles at the next four. Say Bob also attended 5 octas bid tournaments - he got to octas at the first two and didn’t break at the last three.
Intuitively, it seems like Alice is a more successful debater than Bob is. She out-performed Bob at four out of the five tournaments. But Bob qualified, while Alice did not. Why? Because the system discarded useful information. We know that after Alice won her bid round in doubles, she also went on to win in octas, quarters, semis, and finals. The bid system took this information and threw it out for no reason.
Of course, it’s not practicable to factor in all information. Speaker points, for instance, are not significant or consistent enough to make it worth the trouble fitting them into the formula. But surely the difference between a champion and an octafinalist is significant enough to factor in.
Principle #3 - The better a debater does at a tournament, the more points they should get.
Tournaments come in all shapes and sizes. But let’s try to implement this principle in the simplest possible case. Say there is a tournament that has 100 entries, 5 prelims, and then breaks 32 entries to doubles. We’ll call this our Model Tournament.
We know a debater who got to semis should get more points than the debater who got to doubles, but how much more? 4 times more? 1.25 times more? π more? This is a subjective judgement call. When faced with those, it’s better to keep things simple.
The two simplest methods are additive and multiplicative. The additive method increments one’s points by a certain number after every elim win. The multiplicative method multiplies one’s points by a certain factor after every elim win. Of these two, the multiplicative method is worse, because it overemphasizes late elims. Say that we double a debater’s tournament points after every elim win. Then a semifinalist would get 8 times more points than a double-octafinalist, and a champion would get 32 times more points. So a debater who broke to semis once, and then never broke again, would rank higher than a debater who broke to doubles seven times. But what if the tournament where that debater broke to semis had several unusually one-sided resolutions, and the debater was lucky to be on the good side each time? This method runs the risk of one outlier tournament throwing off the entire ranking system.
If we instead use the additive method, how many points should each elim win be worth? The specific number is arbitrary, but as will become clear when we get to Principle #5, it will make the math a lot simpler if it is easily divisible by 2. So let’s say a debater gets 8 points for breaking, and then for each elim they win, they get 4 more points.
Principle #4 - Assume that all tournament fields are equally strong.
Say our Model Tournament took place in Louisiana. On the same weekend, on the other side of the country, a tournament was held in Alaska. The Alaska tournament also had 100 entries, also had 5 prelims, and also broke to doubles. Breaking at the Alaska tournament should then be worth the same number of points as breaking at the Model Tournament.
But what if everyone at the Model Tournament made Demosthenes look like Rick Perry, while all the debaters at the Alaska tournament double-turned themselves in every speech? And what if last year some Louisiana debaters flew out to Alaska and beat everyone at the tournament? Surely, breaking at the Model Tournament should be worth more points?
Wrong. Comparing tournament field strengths is messy and we shouldn’t even try. A national league shouldn’t be in the business of legislating which regions have better debaters. A debater who can afford plane tickets isn’t representative of the average debater in their region. So let’s just assume that all tournaments are equally difficult.
Let’s straighten out a wrinkle though. Say the Model Tournament collapsed its varsity division and its novice division, for a total of 100 entries in the open division. In contrast, the Alaska tournament had 100 entries in varsity, but also an additional 60 entries in novice. How do we bring the two tournaments to a common denominator?
Let’s do a thought experiment - what would happen if the Alaska tournament also decided to collapse its divisions? A rough guess would be that about two thirds of the novice entries would get scared and drop out. The remaining third would try their luck in open. They likely wouldn’t break, but they would beef up the open field size. So a tournament with 100 varsity entries and 60 novice entries is roughly equivalent to a tournament with 120 open entries. This gets to our first actual formula (see XXI.2.A):
(Adjusted Field Size) =
(Open Field Size) +
(Novice Field Size) / (3)
When we compare two tournaments, we should use their adjusted field size (AFS) rather than their open field size.
But now the Alaska tournament has an AFS of 120, while the Model Tournament has an AFS of 100. So breaking at the Alaska tournament should be worth more points. How much more? Keep reading to find out!
Principle #5 - Debaters in the same percentile should get the same number of points.
We’ve figured out how to compare performances at two tournaments with the same AFS. But in reality, tournaments all have different AFSs. How do we bring them to a common denominator?
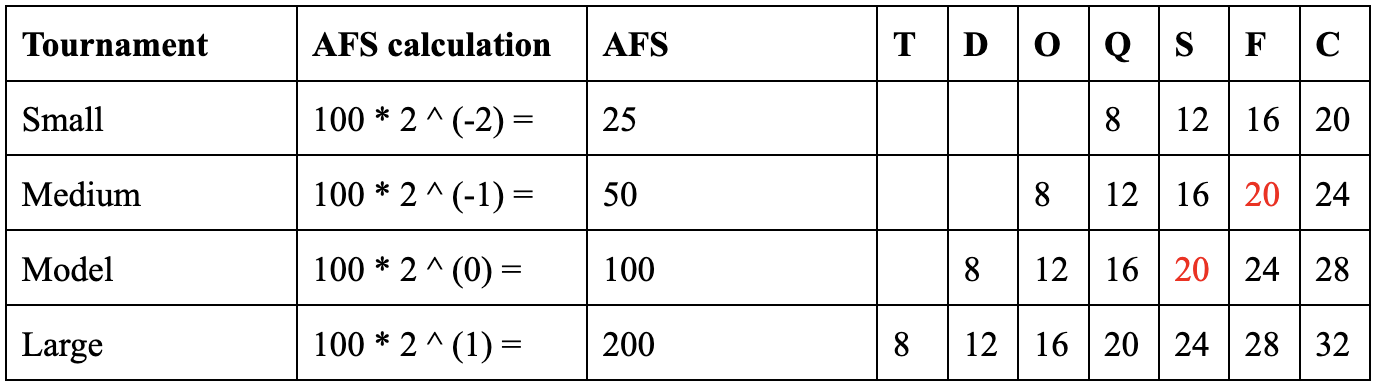
The solution is to look at a debater’s percentile. Say there was a tournament that had 50 entries, 5 prelims, and broke to octas. How many points should we give to a debater who lost in finals of that tournament? We look at their percentile. The finalist was in the top 2 out of 50 entires - that’s the top 4%. Who was in the top 4% of the Model Tournament? It was the semifinalists - they were in the top 4 out of 100. The semifinalists at the Model Tournament got 16 points (8 for breaking, 4 for winning octas, and 4 for winning quarters). So the finalist at the 50-entries tournament should likewise get 16 points.
What is the intuition behind the percentile approach? Say we took the Model Tournament and split it into two pods with 50 entries per pod (like round robins sometimes do). We then break the top 2 entries from each pod and advance them to the semis of the Model Tournament. The pod system is a peculiar tabulation choice, but on average it doesn’t make it any easier or any harder for a debater to get to semis. No matter how you slice it, 4 of the 100 entries will get to semis.
Clearly, getting to finals at a 50-entries tournament is equivalent to being in the top 2 of a 50-entries pod. And being in the top 2 of a Model Tournament pod gets one to the Model Tournament semifinals. So, by transitive property, getting to finals at a 50-entries tournament is equivalent to getting to semifinals at the Model Tournament. Thus both should get the same number of points - 20. Let’s extend this intuition to construct our first points table.
Why are we using powers of 2? Because every elim is two times larger than the next elim - e.g. quarters has 8 entries, semis has 4. The semifinalist at the small tournament is in the top 4/AFS of their field. The quarterfinalist at the medium tournament is in the top 8/AFS of their field. For these two fractions to be equal, the AFS of the medium tournament would have to be exactly two times larger than the AFS of the small tournament.
Let’s straighten out another wrinkle. Is being the champion of a 50-entries tournament equivalent to being the runner-up at a 100-entries tournament? Not exactly. It’s not the equivalent of getting to finals at a 100-entries tournament and then losing. It’s the equivalent of getting to finals at a 100-entries tournament - and then the tournament ending early.
The champion of the 50-entries tournament didn’t get eliminated, but they don’t get to advance to the next elim because there is no next elim. If they did advance to the next elim (i.e. if we imagine their tournament as being a pod of a larger tournament), there’s a 50% chance they would have won it, so let’s give them half of the points for the next elim. In short, we need to adjust our table to give a 2-point bonus to all the champions.
Once we extend this table to apply to all possible AFSs, as shown in this spreadsheet, we’ll arrive at the points table in XXI.2.B.
Principle #6 - A BYE is worth half a win.
Say a debater broke at the Model Tournament, walked over an entry from the same school in doubles (by virtue of being higher seed), and then lost in octas. How many points should this be worth? The debater broke, so they get 8 points for breaking. They lost in octas, so they get 0 points for octas. They didn’t debate in doubles. If they did, there’s a 50% chance they would have won. So let’s give them half of the points for doubles. In total, they get 10 points (8 plus half of 4).
Now let’s say there was a tournament exactly like the Model Tournament, except that it broke straight to octas. How many points should an octafinalist at that tournament get? They skipped doubles (because there were no doubles) and then lost in octas. That’s equivalent to the debater who skipped doubles (due to a walkover) and then lost in octas. So both debaters should get 10 points.
Thinking in this direction, we will eventually come to the conclusion that tournaments that don’t break enough entries should get a points penalty. By skipping early elims, they are functionally giving BYEs in those early elims to the debaters who do break . And a BYE is only worth half a win. Let’s construct a table to calculate what the points penalty should be.
Once we extend this table to apply to all possible break percentages, as shown in this spreadsheet, we’ll arrive at the point penalties listed in XXI.2.D.
Principle #7 - Attending a lot of tournaments should only get you so far.
Say Alice attends 2 model tournaments and wins both of them, getting 30 points each time. Say Bob attends 10 model tournaments and loses in doubles every time, getting 8 points each time. If we add up the points, Alice gets 60, and Bob gets 80. But intuitively, it seems like Alice is the better debater. How do we formalize this intuition?
We could, of course, take the average number of points per tournament. Alice’s average is 30, while Bob’s is 8, so Alice wins hands down. But this would violate Principle #1 - no debater should fall in the rankings because they attended a tournament. If Alice attends a third model tournament and loses in finals, getting 24 points, her average would fall to 28. But we want her ranking to go up, not down.
Instead, let’s take all debaters and compare their single best tournament performance. This is a good comparison, because all ranked debaters attended at least one tournament, so they all have a best tournament.
Second, we take all debaters and compare their second best tournament performance. This is a decent comparison, because almost all debaters have gone to at least two tournaments. But there are a few who haven’t, so let’s discount the second best tournament by 10%.
Third, we take all debaters and compare their third best tournament performance. Now the comparison is starting to get tricky, because lots of debaters didn’t get a chance to attend three tournaments. So if a debater gets 0 points for their third best tournament, it could either be because they didn’t break (that’s a useful data point) or because they didn’t attend (not as useful). We’ll still use this third comparison, because we don’t like discarding data (see Principle #2). But it’s not as good as the first two comparisons - so let’s discount it by 40%.
Eventually, we’ll arrive at the diminishing marginal returns formula from XXI.7.A:
(points from best tournament performance) (1) +
(points from second best tournament performance) (0.9) +
(points from third best tournament performance) (0.6) +
(points from fourth best tournament performance) (0.3) +
(points from fifth best tournament performance) (0.1) =
(total points)